网格去噪与光顺
4 三角形网格的去噪与光顺
扫描设备获取的点云通常有很大噪声, 原本平坦的表面凹凸不平. 我们需要对网格进行去噪 (denoising) 以尽量还原几何体的形状. 一个相似的概念是光顺 (smoothing), 它比去噪更近一步, 删去网格的高频细节, 把网格近一步平滑化.
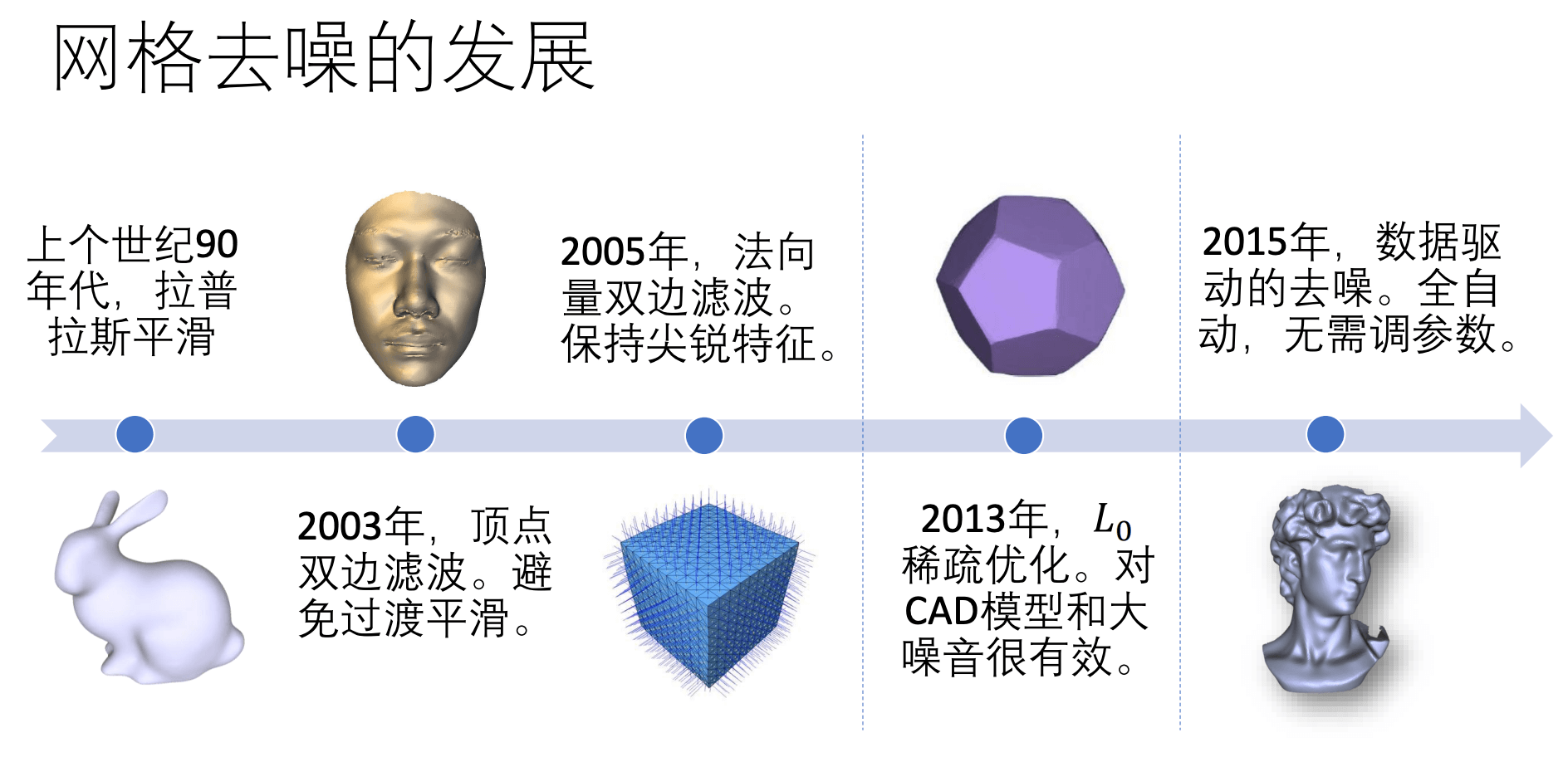
网格去噪算法的发展大致经历了从纯几何算法 (下图第一阶段) 到全局优化算法 (下图第二阶段) 最后到数据驱动的深度学习算法 (下图第三阶段). 图片截自王鹏帅老师的 PPT.
4.1 Laplace 平滑
原论文: Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow, SIGGRAPH 1999.
热传导方程描述了物体的温度场 \(u(x,t)\) 随时间的变化: \[ \pdv{u}{t} = \lambda\Delta u. \] (参数 \(\lambda>0\)) 温度场随时间会逐渐变得平滑. 受到热传导方程的启发, 我们可以用类似的思路进行网格平滑.
热传导方程在曲面 \(\Sigma\subset\R^3\) 上的版本由曲面的 Laplace-Beltrami 算子 \(\Delta\) 给出: \[ \pdv{f}{t} = \lambda\Delta f, \] 其中 \(f:\Sigma\to\R\) 是曲面上随时间演化的可微函数, 它会越来越平缓. 特别地, 将曲面的浸入 \(F:\Sigma\to\R^3\) (它给出了曲面上每一点的三维坐标) 代入: \[ \pdv{F}{t} = \lambda\Delta F, \] 便可以让曲面变得平滑.
实际上, \(\Delta F=2Hn\), 其中 \(n\) 是单位法向量场, \(H\) 是曲面的平均曲率 (mean curvature). 直观上看, \(Hn\) 指向 "曲面弯曲得最厉害的方向"
对于球面/柱面来说, \(Hn\) 指向内部; 对于标准 (主轴长相等) 双曲抛物面来说, \(Hn\) 在中心处为零. 平均曲率为零意味着该点是曲面的 "鞍点". [1].因此, 热传导方程化为 \[ \pdv{F}{t} = \frac{\lambda}{2} Hn. \] (称为平均曲率流) 从几何上来看, 它使得曲面沿着其法向演化, 并减小曲面的表面积; 该方程的稳态满足 \(\Delta F=0\), 即 \(H=0\). 此时的曲面称为极小曲面 (minimal surface), 因其表面积取极小值
将铁丝弯成封闭曲线, 浸入肥皂水, 肥皂薄膜形成的曲面就是极小曲面. [2].
总之, 如果我们有三角形网格 \({\cal
K}\), 其顶点集为 \(\{x_i\}\),
那么我们可以应用离散化的平均曲率流 \[
x_i^{(k+1)} = x_i^{(k)} + \tau\Delta x_i^{(k)},
\] 其中 \(x_i^{(k)}\) 表示时间
\(k\) 时的位置; \(\tau>0\) 为步长; \(\Delta x_i^{(k)}\) 是 \(x_i\) 处 (离散) Laplace-Beltrami
算子的结果. 上式是显式 Euler 方法, 容易导致数值不稳定.
我们将其替换为隐式 Euler 方法: \[
\Align{
x_i^{(k+1)} &= x_i^{(k)} + \tau\Delta x_i^{(k+1)}, \\
\textsf{即}\quad
({\rm id} - \tau\Delta) x_i^{(k+1)} &= x_i^{(k)}.
}
\] 这是一个线性方程 (注意到 \(\Delta\) 的 uniform formula 或 cotangent
formula 都是 \(x_i^{(k+1)}\) 的一次式
- 迭代步长 \(\tau\) 和迭代次数 \(K\) 需要手动调整.
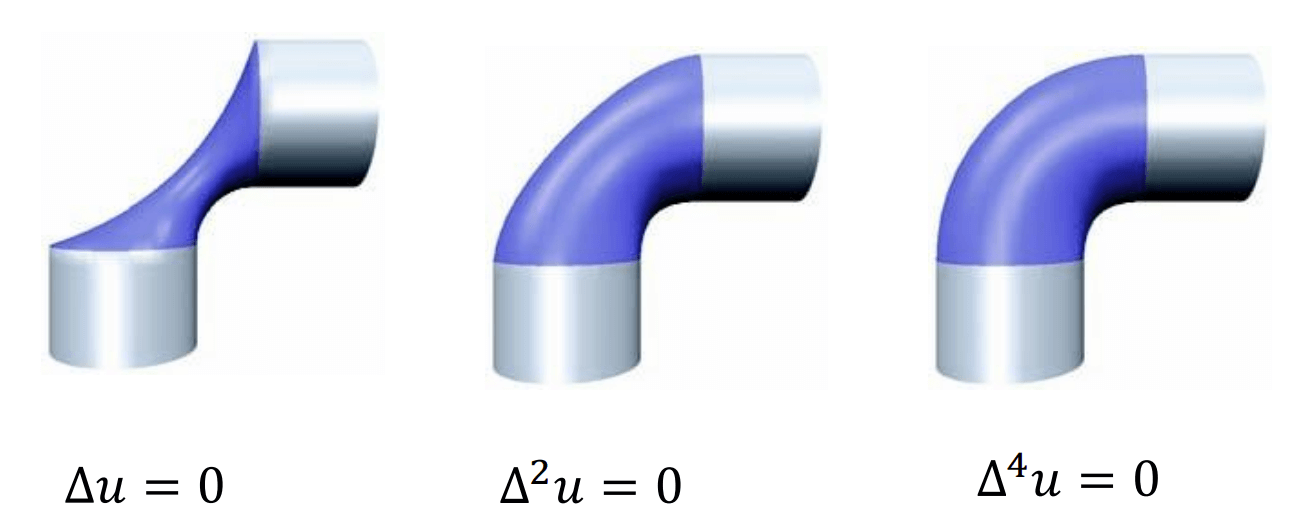
另外, 也可以使用高阶 Laplacian: \[
\pdv{F}{t} = \lambda\Delta^k F,
\] 它们通常能取得更好的结果, 但是计算成本较高, 故不常用.
下图展示了高阶 Laplacian 的稳态解, 它们能达到更好的平滑效果 (图源课程
PPT
4.2 顶点双边滤波
原论文: Bilateral Mesh Denoising, SIGGRAPH 2003.
Laplace 平滑可以把噪音去除, 但是也会抹去几何体原本的细节信息 (如果用 uniform formula, Laplace 平滑实际上就是让顶点坐标趋于附近顶点的均值, 类似于 Gauss 模糊). 为此引入双边滤波, 避免过度平滑.
先从图像的双边滤波讲起. 设图像 \(I\), 它的双边滤波可以在去除噪声的同时保持边缘: \[ I'(x) := \frac1{K_x} \sum_{y\in N(x)} \underbrace{G_{\sigma_s} (\|y-x\|)}_{\textsf{space/domain kernel}} \cdot \underbrace{G_{\sigma_r} (\|I(y)-I(x)\|)}_{\textsf{range kernel}} \cdot I(y). \] 其中 \(G_{\sigma_s},G_{\sigma_r}\) 是两个正态分布, \(N(x)\) 是 \(x\) 的邻域, \(K_x\) 是归一化项. 双边滤波在 Gauss 模糊的基础上添加了 range kernel: 如果 \(x,y\) 像素差异过大, 则 range kernel 的值极小, 进而 \(I(y)\) 的贡献几乎为零, 不会让边缘变得模糊.
该论文将双边滤波引入网格去噪. 然而, 我们的待去噪函数 (即图像的 \(I(x)\)) 恰好就是网格位置 \(x\), 如果直接代入会导致双边滤波退化为 (类) Gauss 模糊: \[ x' = \frac1{K_x} \sum_{y\in N(x)} G_{\sigma_s}(\orange{\|y-x\|})G_{\sigma_r}(\orange{\|y-x\|})y. \] 为此, 我们不去对 \(x\) 进行双边滤波, 而是对高度图进行双边滤波. 设顶点 \(x\) 具有单位法向量 \(n\), 其邻域内的点 \(y\in N(x)\) 的 "高度" 定义为法向上的位移: \[ h(y) := \lr{n, x-y}. \] 把 \(h\) 作为 \(I\) 代入双边滤波公式即可. 双边滤波网格去噪算法十分容易实现, 不需要解方程, 也不需要计算 Laplace-Beltrami 算子, 只需要做迭代即可.
4.3 法向双边滤波
原论文: Feature-Preserving Mesh Denoising via Bilateral Normal Filtering, CAD-CG 2005.
该论文发现, 直接对法向量 \(n\) 进行双边滤波的效果要好于对高度图 \(h\) 进行双边滤波: \[ n'_i := \frac1{K_i} \sum_{T_j\in N(T_i)} {G_{\sigma_s} (\|c_j-c_i\|)} \cdot {G_{\sigma_r} (\|n_j-n_i\|)} \cdot n_j. \] (其中三角形 \(T_i\) 的中心为 \(c_i\), 法向量为 \(n_i\).) 尖锐的区域两侧的法向量差别很大 (与高度图相比), 滤波后易于保持尖锐特征. 该算法迭代地对法向量进行滤波, 每次滤波过后需要调整三角形顶点的位置. 为了让三角形 \(T=(x_i,x_j,x_k)\) 的法向量尽量接近滤波后的法向量 \(n\), 考虑优化问题 \[ \min_{x_i,x_j,x_k} \sum_{\sf cyc} \lr{n,x_i-x_j}^2. \] 最终的目标是使 \(n\) 和每条边 \(x_i-x_j,\dots\) 尽量接近垂直. 我们用梯度下降法求解这个优化问题: \[ x_i' = x_i + \lambda \sum_{T\ni x_i} \sum_{(x_k,x_l)\in T} \lr{n_T,x_k-x_l} n_T. \] 双边滤波法需要手动调整的参数包括方差 \(\sigma_s^2,\sigma_r^2\) 和迭代次数.
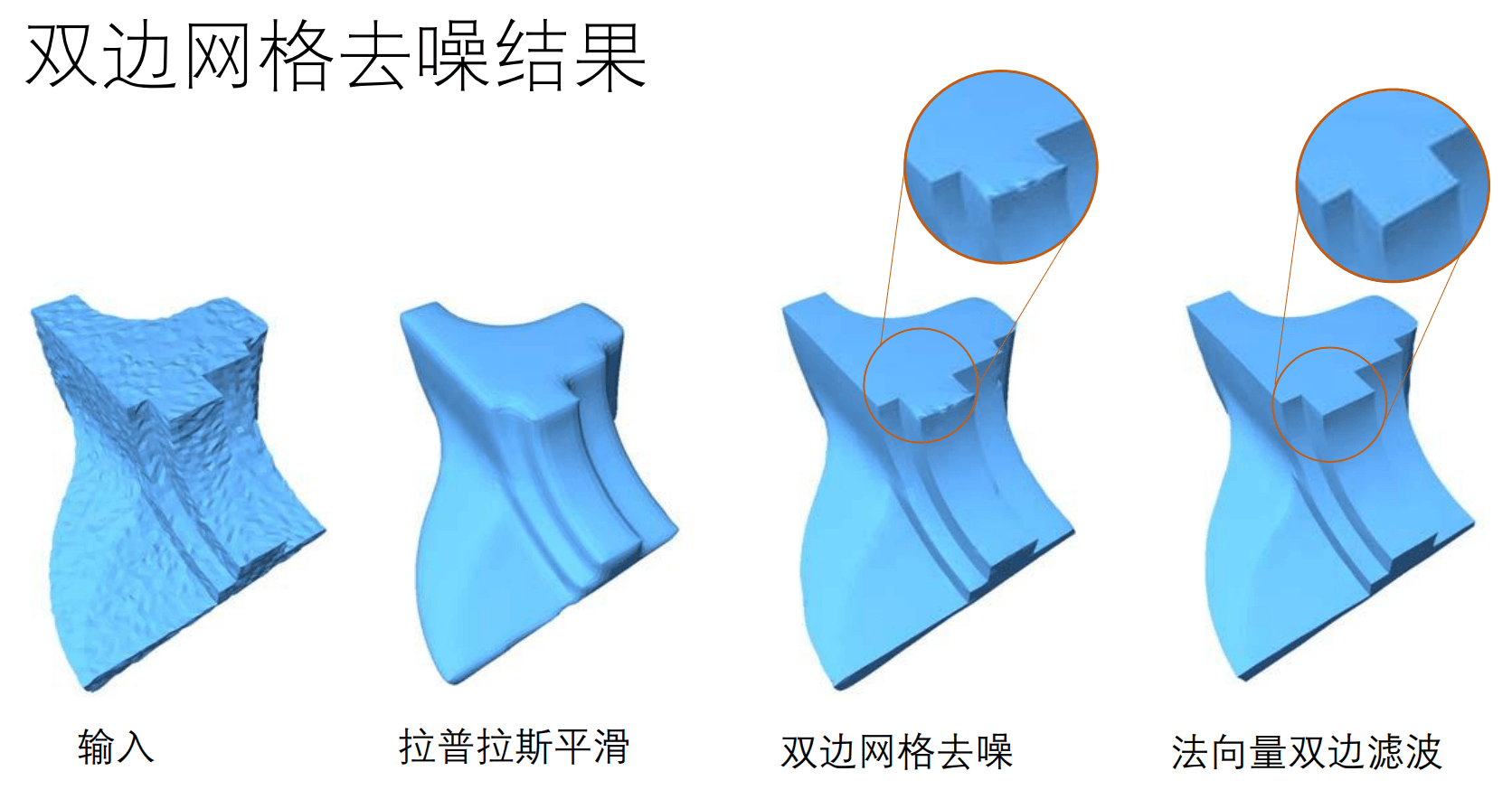
可以看到, 对于一般的噪声, 法向双边滤波已经可以取得令人满意的结果 (图自课程 PPT, 原图自原论文).
双边滤波的近一步改进方法是联合双边滤波 (joint bilateral filter), 用一个 "指导曲面" 作为 range 的 difference: \[ n'_i := \frac1{K_i} \sum_{T_j\in N(T_i)} {G_{\sigma_s} (\|c_j-c_i\|)} \cdot {G_{\sigma_r}(\|\orange{\tilde{n}_j-\tilde{n}_i}\|)} \cdot n_j. \] 联合双边滤波的效果十分依赖指导曲面的选取. 一个简单的选择是 Gauss 模糊后的法向量: \[ \tilde{n}_i := \frac1{K'_i}\sum_{T_j\in N(T_i)}G_\sigma(\|c_j-c_i\|)n_j. \]
4.4 \(L_0\) 稀疏优化
原论文: Mesh Denoising via \(L_0\) Minimization, SIGGRAPH 2013.
图像处理中有稀疏优化的问题: 优化图像 \(I^*\) 的梯度, 使之尽可能稀疏: \[ \min_I \pqty{ \|I-I^*\|_2^2 + \lambda\|\nabla I\|_0 }. \] 所谓 "尽可能稀疏" 可以用 \(\ell^0\) 范数衡量: \(\|v\|_0\) 等于 \(v\) 的非零分量的个数. 因此, 上式的含义是, 保持 \(I\) 尽量和原图 \(I^*\) 接近的条件下, 使梯度尽可能都等于零.
然而上式不可微, 难以直接优化. 一个巧妙的办法
\[ \min_{I,\delta} \pqty{ \|I-I^*\|_2^2 + \beta \|\nabla I-\delta\|_2^2 +\lambda \|\delta\|_0 }. \]
只需交替进行两个步骤:
- 固定 \(I\), 优化 \(\min_{\delta}\pqty{\beta\|\nabla I-\delta\|_2^2+\lambda \|\delta\|_0}\). 这个式子关于 \(\delta\) 是 pixelwise 的, 因此对每个像素分别优化即可.
- 固定 \(\delta\), 优化 \(\min_{I}\pqty{\|I-I^*\|_2^2 + \beta \|\nabla I-\delta\|_2^2}\). 这是一个二次式, 可以通过梯度下降或者最小二乘法来优化.
可以把它推广到三维的三角形网格. 我们构造优化问题 \[ \min_c \pqty{ \|p-p^*\|^2 + \lambda\|D(p)\|_0 }, \] 其中微分算子 \(D(p)\) 的选择是一个问题. 首先, 梯度 \(\nabla p\) 是不可行的, 因为梯度为零意味着 \(p\) 为常值, 即 mesh 退化为一点. 其次, Laplace-Beltrami 也不可行, 因为稀疏的 Laplacian 迫使曲面向极小曲面演化 (下图右侧展示了稀疏化 Laplacian 的结果; 图自原论文).

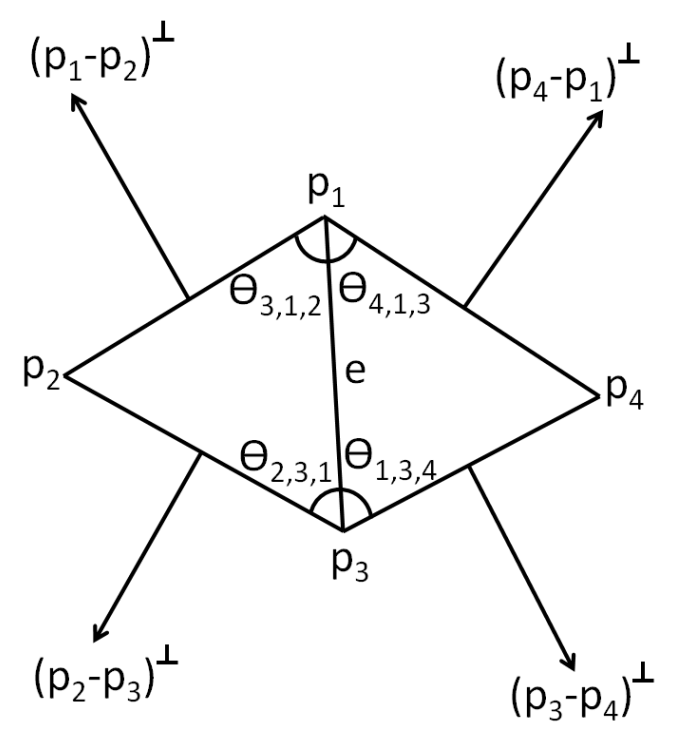
论文提出了一种新的离散微分算子——边上的 Laplacian. 类似于顶点 Laplacian 的 cotangent formula 的推导, 边上 Laplacian 的公式为 \[ D(e) = \pmqty{ - \cot\theta_{2,3,1} - \cot\theta_{1,3,4} \\ \cot\theta_{2,3,1} + \cot\theta_{3,1,2} \\ - \cot\theta_{3,1,2} - \cot\theta_{4,1,3} \\ \cot\theta_{1,3,4} + \cot\theta_{4,1,3} }\T \pmqty{ p_1\\p_2\\p_3\\p_4 }. \] 相关记号见下图 (图自原论文).
几何上看, \(D(e)\) 的模长为 \(2\sin(\gamma/2)\cdot\|p_1-p_3\|\), 其中 \(\gamma\) 是两个三角形组成的二面角大小. 当 \(\gamma<\pi/2\) 时, \(2\sin(\gamma/2)\) 可以较好地估计 \(\gamma\), 因此 \(\|D(e)\|\) 可以作为平均曲率的估计.
稀疏优化方法在强噪音下表现良好, 如下图 (图自课程 PPT, 原图自原论文).

然而, 该方法也需要调参, 需要一个合适的 \(\lambda\) 来平衡去噪与细节保持.
4.5 数据驱动的去噪
原论文: Mesh Denoising via Cascaded Normal Regression, SIGGRAPH Asia 2016.
以上的所有方法都需要手动调参, 能否使用数据驱动的机器学习来自动进行网格去噪?
除了不用调参之外, 数据驱动的方法还有另外一个优势——即无需对数据做先验假设. 三角形网格去噪是一个欠定的问题: \[ \underbrace{\textsf{有噪网格}}_{\textsf{已知}} = \underbrace{\textsf{干净网格}}_{\textsf{未知,待求}} + \underbrace{\textsf{噪音}}_{\textsf{未知}}, \] 其中干扰变量噪音和干净网格都是未知的. 我们当然可以对其做出一些假设 (例如线性回归假设噪音服从正态分布), 前人的方法或多或少都有一些假设:
- Laplace 平滑和 \(L_1\)-analysis (Wang et al. 2015) 都假设噪音是独立同分布的.
- 法向双边滤波和 \(L_0\) 稀疏优化都假设三角形网格是逐片平滑的 (片与片有清晰的边界).
然而, 噪音源和网格的几何特征都是多变的, 可能不满足这些先验假设. 而数据驱动的算法可以从数据中学习先验, 以得到更好的去噪结果与泛化能力.
4.5.1 Descriptors
具体来说, 该论文利用机器学习方法从噪音网格中恢复真实的法向量 (这可能是最早将数据驱动的方法应用到 3D 几何领域的工作之一了). 模型的设计受到了法向双边滤波调参过程的启发. 对于有噪音的网格 \(M\), 我们选取若干组方差 \((\sigma_{s_1},\sigma_{r_1}),\dots,(\sigma_{s_k},\sigma_{r_k})\), 分别应用对应的 bilateral filter 到三角形 \(T_i\) 的法向量 \(n_i\) 上, 得到各个尺度的双边滤波结果, 并将它们打包: \[ \pqty{ n_i(\sigma_{s_1},\sigma_{r_1}),\dots,n_i(\sigma_{s_k},\sigma_{r_k}) }. \] 再对这 \(k\) 个法向量迭代地应用 (对应方差的) bilateral filter, 得到 \(K\) 组: \[ S_i := \pqty{ n_i^{(1)}(\sigma_{s_1},\sigma_{r_1}),\dots, n_i^{(1)}(\sigma_{s_k},\sigma_{r_k}), \dots, n_i^{(K)}(\sigma_{s_1},\sigma_{r_1}),\dots, n_i^{(K)}(\sigma_{s_k},\sigma_{r_k}), }, \] 即为三角形 \(T_i\) 的描述子 (称为 B-FND). 对应地, 还有联合双边滤波版本的描述子 \(S_i^g\) (称为 G-FND).
FND 描述子是平移不变的 (平移不改变法向量), 但在旋转下会变化. 为了让 FND 旋转不变, 需要对齐主方向 (类似图像的 SIFT 特征).
4.5.2 Cascaded regression
模型采用单隐层神经网络拟合 \(S_i\mapsto n_i^{g}\) (gound truth) 的非线性映射, 损失函数为平方损失: \[ \min_{\Theta} \sum_i \| F(S_i;\Theta) - n_i^g \|^2. \] 论文将若干 "特征提取 \(\Rightarrow\) 单隐层回归" 串联起来, 得到了一个级联 (cascaded) 回归模型, 如下图 (图自课程 PPT). 以上一个回归的输出作为下一层的输入, 可以逐渐减小误差并得到更好的结果.
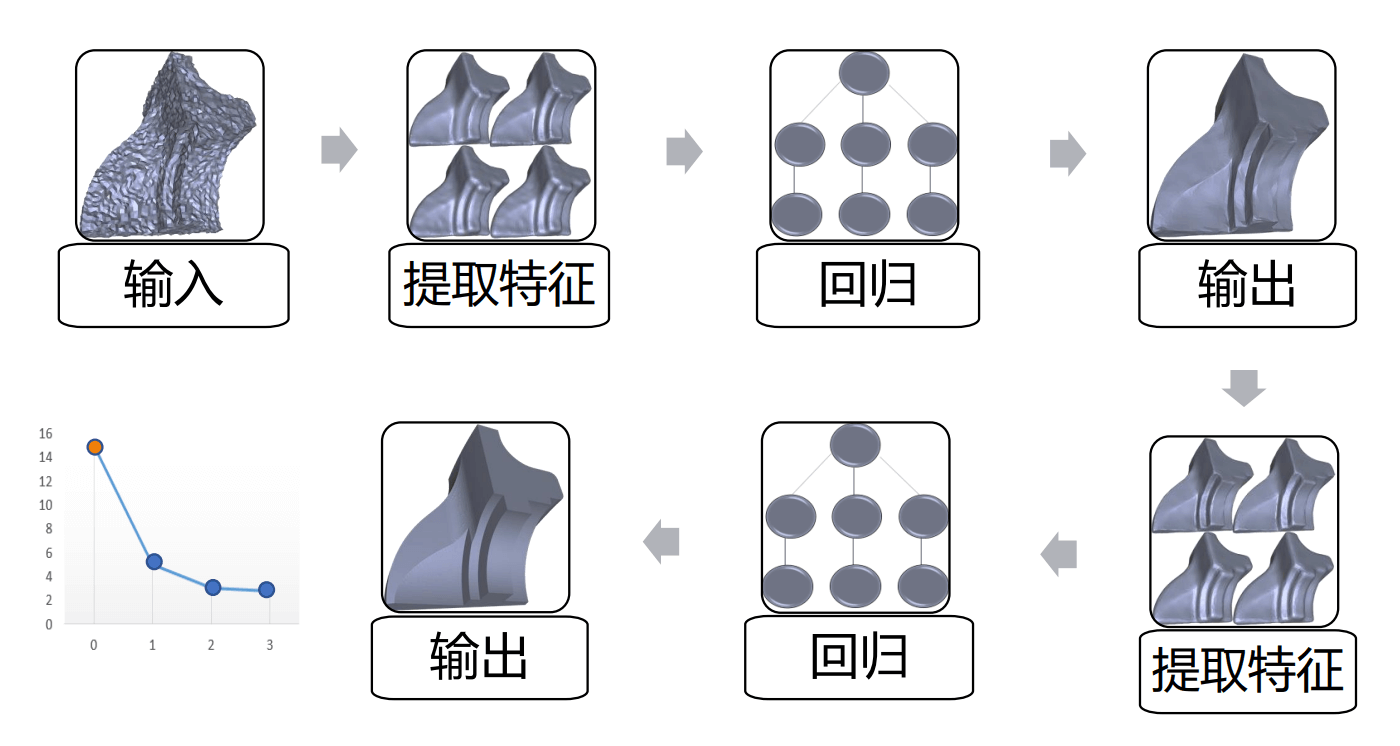
4.5.3 K-means clustering
由于三角形网格不同区域的 descriptors 通常差别很大, 对所有 descriptors 都用同一个神经网络是不合适的. 我们可以先对 descriptors 进行 K-means 聚类, 对每个类别中的 descriptors 分别使用一个神经网络 (类似于 mixture-of-experts 技术).
下图展示了在不同噪声种类与强度下, B-FND 和 G-FND 特征聚类的结果 (图自原论文).
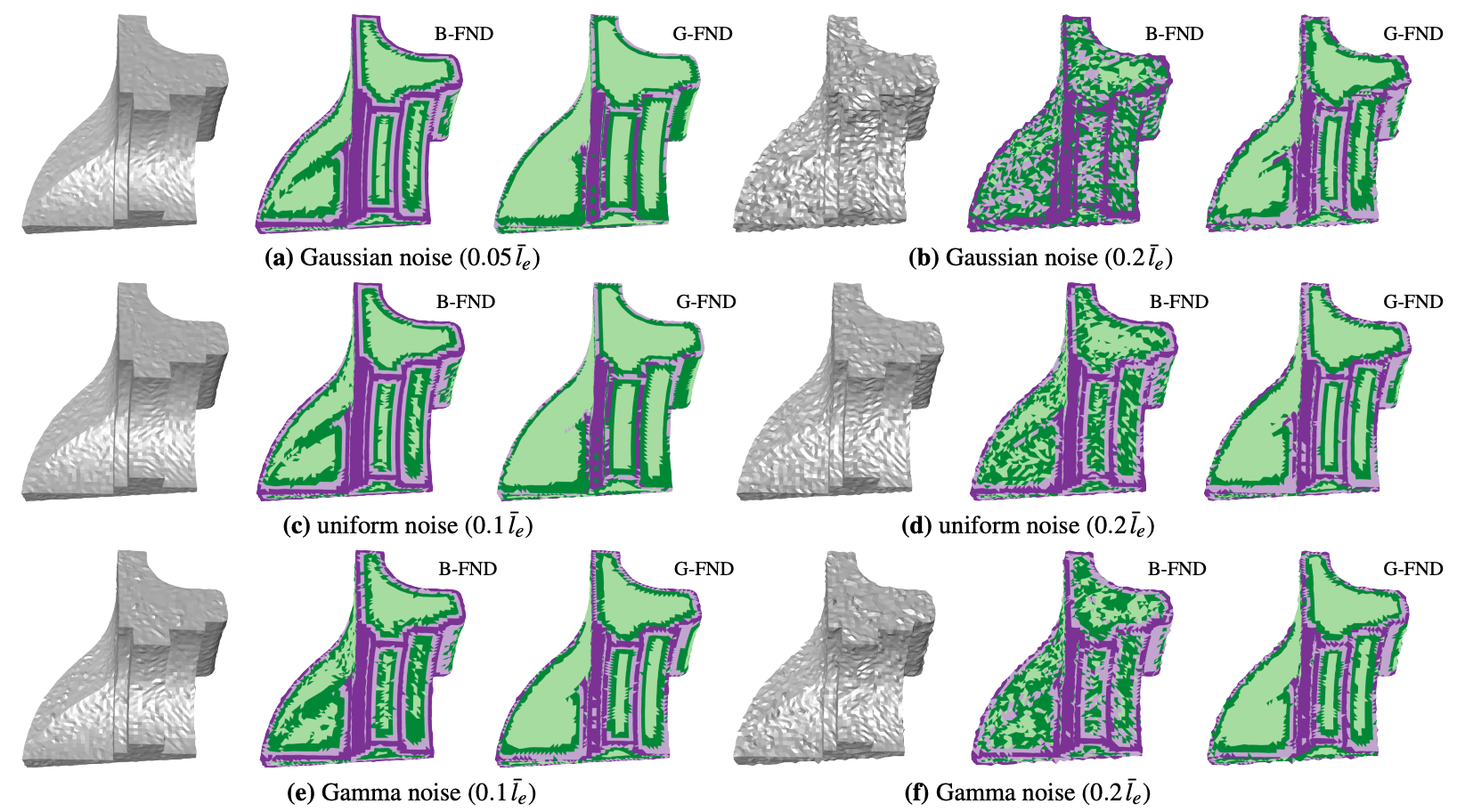
4.5.4 Results
这篇论文其实是王鹏帅老师在微软亚洲研究院时作出的成果. 为了测试算法在真实 3D 模型上的表现, 他们团队还用 Kinect 手动扫描了很多石膏模型, 做成了三个数据集. (图自课程 PPT, 原图自原论文.)
