几何表示
1 几何表示的几种方法
如何在计算机内表示/存储一个三维的几何体? 比如下面的 Stanford Bunny.

在数学上, 我们可以用函数的水平集 (比如方程 \(F=0\) 的解集) 或者参数曲面来表达一个几何体. 然而现实中的几何体一般都复杂到难以写出具体的解析式. 因此, 我们只能利用一些近似手段, 将几何体 (或者其表面) 的近似形态存储在计算机里.
最直接的办法是用若干固定大小的小立方体, 像搭积木一样砌成几何体形状.
这被称为体素表示 (voxel representation) (下图最中间,
图源 Research Gate
另一种比较直接的方法是在几何体表面采样很多很多点, 称为点云 (point cloid), 用这些点拟合几何体的表面 (下图左).
为了表示几何体的表面, 还可以采用多边形网格 (polygon mesh), 即用若干多边形 (一般是三角形) 组成的一张 "网" 拟合几何体的表面 (下图右, 三角形网格).

受到隐函数曲面 (比如球面 \(x^2+y^2+z^2-r^2=0\)) 的启发, 我们可以用符号距离场 (signed distance field, SDF) 表示几何体的表面. 对于空间中的每一点 \(x\), SDF 给出了 \(x\) 到几何体表面的有符号距离 (几何体内部为负, 外部为正, 表面上为零; 当然内外也可以反过来). 下图是 bunny 的 SDF (图源课程 PPT).

上面四种表示方法中, 体素、点云、多边形网格称为显式表达, 符号距离场称为隐式表达. 它们对应了不同的应用场景, 并且可以相互转换.
Polygon mesh processing (Mario Botsch et al.) Section 1.6 中总结显式表达和隐式表达如下:
Parametric surfaces can capture even the finest detail, are easy to sample, and can be modified intuitively but it is difficult to answer distance queries and topological changes require a major restructuring. On the other hand, topological changes and distance queries are easy for implicit surfaces but sampling and shape editing is not straightforward and the geometric detail resolution depends on the voxel size.
我们目前只介绍一些最基本的表示方法. 一些先进的方法, 比如八叉树 (体素的升级版, 实现自适应分辨率), radiance field, 3D Gaussian 等将在之后特定 topic 中介绍.
1.1 三角形网格
严格地说, 一个多边形网格指的是 \(\R^3\) 中有限个多边形的集合 \({\cal K}\), 满足:
- \({\cal K}\) 中任意两个多边形或者不交 (交集为空), 或者有公共边/公共顶点.
多边形 \(P\in{\cal K}\) 也称为一个 "多边形面片 (polygon facet)". 三角形是最基本的多边形, 任意多边形网格 \({\cal K}\) 可以通过切割面片的方式化为一个三角形网格. 下面我们主要研究三角形网格.
三角形网格的表达能力很强, 任意二维拓扑流形都能表达为三角形网格 (当然也能表示一些非流形的几何体), 而且三角形网格能表达细致的几何信息, 也容易编辑. 三角形网格的另一个好处是经典微分几何中的曲面理论能直接推广到三角形网格.
1.1.1 Local averaging region
由于三角形网格是分片线性的, 在交界处不可微, 故顶点 \(v\) 处的微分量不能直接计算. 一种办法是计算微分量在 \(v\) 的一个邻域内的平均值. 这样的邻域称为局部平均区域 (local averaging region). 下图展示了几种不同的 local averaging regions: (图源 Polygon mesh processing, Figure 3.7)

- Barycentric cell: 顶点 \(v\) 周围一圈三角形的重心和边的中点连成的多边形.
- Voronoi cell: 顶点 \(v\) 周围一圈三角形的外心连成的多边形. (该区域内任意一点 \(p\) 到 \(v\) 的距离不大于 \(p\) 到其他顶点的距离).
- Mixed Voronoi cell: 和 Voronoi cell 差不多, 只不过如果外心在三角形外, 则用边的中点代替.
在近似精度上, mixed Voronoi cell 最佳, Voronoi cell 次之.
1.1.2 法向量
顶点 \(v\) 处的单位法向量定义为周围一圈三角形的法向量之平均值: \[ n(v) := \frac{ \sum_{T\in{\cal N}_1(v)}\alpha_T n(T) }{ \|\sum_{T\in{\cal N}_1(v)}\alpha_T n(T)\| }, \] 其中 \({\cal N}_1(v)\) 是以 \(v\) 为顶点的三角形的集合, \(\alpha_T\) 为三角形 \(T\) 的权重, 通常有如下几种选择:
- 常值 \(\alpha_T\equiv1\), 方便计算但并未考虑网格的几何.
- 面积 \(\alpha_T=|T|\), 比较方便, 但仍会导致一些反直觉结果.
- 顶角 \(\alpha_T=\theta_T\) (即 \(T\) 在 \(v\) 处的内角), 需要反三角函数, 计算量大, 但是效果很好.
对大多数应用场景, \(\alpha_T=\theta_T\) 都是不错的选择.
1.1.3 梯度
记三角形 \(T\) 的三个顶点为 \(v_i,v_j,v_k\), 分片线性函数 \(f\) (在每个三角形上是线性的) 在顶点处的值 \(f_i,f_j,f_k\), 则函数值在三角形内的值为 \[ f(x) = \frac{A_i(x)f_i + A_j(x)f_j + A_k(x)f_k}{A},\quad x\in T, \] 其中 \(A_i(x),A_j(x),A_k(x)\) 为三个小三角形的面积, \(A\) 为整个三角形的面积, 如下图.

- 实际上, \(x=(A_i/A)v_i+(A_j/A)v_j+(A_k/A)v_k\). 系数 \((A_i/A,A_j/A,A_k/A)\) 称为 \(x\) 的重心坐标 (barycentric coordinates).
三角形面积等于底边长乘以高, \[ \Align{ B_i(x) &= \frac{ \lr{(x-v_j),\frac{(v_k-v_j)^\perp}{\|v_k-v_j\|}} \|v_k-v_j\| }{2A} \\ &= \frac{ \lr{(x-v_j),(v_k-v_j)^\perp} }{2A}, } \] (其中 \((\cdot)^\perp\) 表示 \((\cdot)\) 逆时针旋转 \(\pi/2\) 得到的向量) 有 \(\nabla B_i(x) = \frac{(v_k-v_j)^\perp}{2A}\), 于是 \(f\) 的梯度为 \[ \nabla f(x) = \sum_{\sf cyc} f_i \nabla B_i(x) = \frac1{2A} \sum_{\sf cyc} f_i (v_k-v_j)^\perp. \] 可以发现 \(\nabla f\) 与 \(x\) 无关, 即在三角形 \(T\) 上是常数. 这是 \(f\) 的分片线性性的必然结果.
1.1.4 Laplace-Beltrami 算子
1.1.5 数据结构
最后说说怎么把三角形网格存储在计算机里.
面表: 需要一个顶点列表 \(\{(x_1,y_1,z_1),(x_2,y_2,z_2),\dots\}\)
和三角形列表 \(\{(i_1,j_1,k_1),(i_2,j_2,k_2),\dots\}\).
顶点列表记录每个顶点的坐标, 三角形列表记录每个三角形由哪些顶点组成
(顶点索引). 使用面表存储 mesh 的文件格式有 .obj,
.off 等.
半边: 将每条边拆成两条有向半边 (halfedge), 方向相反.
每条半边只属于一个面片, 并且我们要求每个面片中的三条半边首尾相接
(呈顺时针/逆时针方向)
下图中, 每个三角形的三条半边都呈现逆时针方向 (蓝色箭头). 我们规定三角形法向量的方向应当与蓝色箭头满足 "右手螺旋定则" (右手握拳并竖起大拇指, 四指的方向与蓝色箭头相同, 则拇指指向法向; 在下图中, 法向量指向屏幕外).
每条半边 (以下图橙色边为例) 存储了如下数据:
- 它指向的顶点, 下图 1.
- 它的另一半, 下图 2.
- 它相邻的面, 下图左边的三角形.
- 它在该三角形中的下一条边, 下图 3.
- 它在该三角形中的上一条边, 下图 4 (非必需, 因为可通过上述操作组合得到, 比如下下条边).

此外, 每个顶点还保存了它的坐标以及从它出发的某一条半边. 每个面保存了它的某一条半边.
从顶点 \(v\) 出发, 可以在常数时间内遍历其 \(1\)-邻域 (所有与 \(v\) 相邻的三角形) \({\cal N}_1(v)\):
- 获取从 \(v\) 出发的某条半边 \(e_1\). (半边 \(e_1\) 的相邻面便是 \({\cal N}_1(v)\) 的第一个元素.)
- 获取 \(e_1\) 的另一半 \(e_2\).
- 获取 \(e_2\) 的下一条边 \(e_3\). (半边 \(e_3\) 的相邻面便是 \({\cal N}_1(v)\) 的第二个元素.)
- 以此类推, 获取 \(e_4,e_5,\dots\), 直到回到 \(e_1\).

1.2 点云
点云是最容易表示与存储的, 只需列出每个点的坐标即可. 点云也是最容易获得的, 使用一个深度传感器获取深度图, 再根据相机参数将点的深度转化为点坐标即可. 一般会对物体的各个侧面分别构建点云, 然后将它们合并起来. 将几个小点云合成一个大点云的过程称为点云配准 (registration). 下图展示了将两个点云 (黑色和蓝色) 对齐的过程 (图源 Wikimedia).

1.2.1 ICP
ICP (iterative closest point) 是一种迭代的点云配准算法. 算法假设两个点云 \(P=\{p_i\}\) 和 \(Q=\{q_i\}\) 可以用刚体变换 (平移, 旋转, 反射) 对齐. 设刚体变换为 \(p\mapsto Rp+t\) (\(R\) 为正交阵). 算法迭代地优化 \(R,t\), 具体流程如下:
- 利用 PCA 初始化 \(R,t\).
- 将 \(p_i'=Rp_i+t\) 与离它最近的 \(q_i\) 匹配.
- 丢弃距离大于 \(k\) 倍中位距离的点对 (outliers).
- 构造误差函数 \(E=\sum_i\|Rp_i+t-q_i\|^2\) (点对距离的平方和).
- 利用 SVD 分解最小化 \(E\), 解出新的 \(R,t\).
重复以上 2-5 步, 直到误差 \(E\) 足够小, 便得到了我们想要的 \(R,t\).
ICP 的可视化见此网站.
1.2.2 法向量
由于传感器生成的点云具有很规则的空间排布, 即在成像平面为矩形点列, 我们可以据此直接构建一个三角形网格 (如下图, 图源课程 PPT), 为每个三角形计算法向量, 再插值得到顶点法向量.

另一种比较通用的计算点云法向量的方法见下文 "SDF 曲面重建" 中的 MLS 方法.
2 几种表示的转换
\[ \xymatrix@!{ &&& *[F-,]{\textsf{三角形网格}} \\ *[F-,]{\textsf{实际场景}} \ar[r]^-{\textsf{传感器}}_-{\textsf{点云配准}} & *[F-,]{\textsf{点云}} \ar@/^1.2pc/@<0ex>[rru]^-{\textsf{显式曲面重建}} \ar@/_1.2pc/@<0ex>[rrd]_-{\textsf{隐式曲面重建}} \\ &&& *[F-,]{\textsf{符号距离场}} \ar@<0.0ex>[uu]^{\substack{\textsf{Marching}\\\textsf{cubes}}} } \]
2.1 Marching Cubes
Marching cubes 算法将空间中的 SDF 转化为三角形网格.
原论文: Marching cubes: A high resolution 3D surface construction algorithm.
2.1.1 想法
我们首先将空间离散化为 \(n^3\) 个边长为 \(d\) 的正方体 grid (下图左). 如果正方体足够小, 且曲面 \(\Sigma\) 足够光滑, 那么曲面 \(\Sigma\) 与每个正方体的交集应可以用若干三角面片近似 (下图右, 橙色的球面和正方体的交集近似为一个梯形, 可由两个三角形拼成).
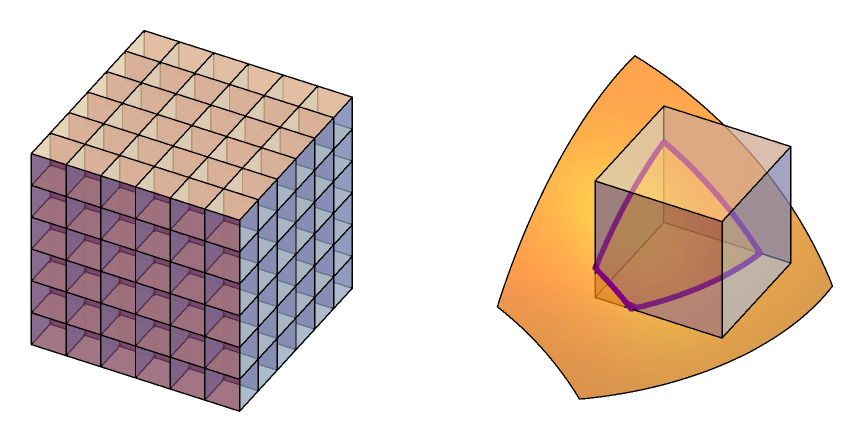
具体来说, 对于一条边 \(e=(p_0,p_1)\), 如果 \({\sf SDF}(p_0)\cdot{\sf SDF}(p_1)\leq0\), 我们就认为曲面 \(\Sigma\) 与边 \(e\) 有一个交点. 由于每个顶点的 SDF 都有两种情况 (正或负), 一个正方体一共有 \(2^8=256\) 种情况; 模去对称性后剩下 \(15\) 种情况: (图源 Wikimedia)

我们不妨假设 SDF 在边 \(e\) 上近似为线性函数, 则交点的坐标为 \[ v = \frac{-F_1}{F_0-F_1} p_0 + \frac{F_0}{F_0-F_1} p_1, \] 其中 \(F_i={\sf SDF}(p_i)\), \(i=0,1\).
该算法逐个遍历每个正方体, 计算完一个后行进到下一个, 故得名 "行进立方体" (marching cubes).
2.1.2 查表
在实现上, 如何快速确定哪些边上有交点/哪些交点属于同一个三角形? 答案是查表.
构造一个 \(8\) 位二进制数 \(\sf vertexState\), 其第 \(i\) 位表示第 \(i\) 顶点的 SDF 是否大于零. 用 \(\sf vertexState\) 作为索引查表, 得到一个 \(12\) 位的二进制数 \(\sf edgeState\), 它的第 \(i\) 位表示第 \(i\) 条边上是否有要生成顶点.
计算出交点坐标后, 再次利用 \(\sf vertexState\) 作为索引, 查另一张表, 得到一个集合 \[ \{(i_1,j_1,k_1),(i_2,j_2,k_2),\dots\}, \] 集合的每一个元素 \((i,j,k)\) 代表一个三角形, \(i,j,k=1,\dots,12\) 分别表示三角形顶点所在的边. 由此便得到了该正方体中的所有三角形面片.
因此, 算法需要两张长度为 \(2^8=256\) 的表, 分别给出 edge state 和 set of triangles.
2.1.3 法向量
最后, 我们还需要计算三角形顶点处的法向量. 因为有 SDF, 我们可以直接利用 SDF 的梯度计算法向量, 而无需在 mesh 上进行插值.
首先计算 cube 顶点 \(p=(i,j,k)\) 处的梯度 \(G(i,j,k)\). 由 central difference 公式, 梯度的三个分量分别为 \[ \Align{ G_x(i,j,k) &= \frac{G(i+1,j,k)-G(i-1,j,k)}{2d}, \\ G_y(i,j,k) &= \frac{G(i,j+1,k)-G(i,j-1,k)}{2d}, \\ G_z(i,j,k) &= \frac{G(i,j,k+1)-G(i,j,k-1)}{2d}. } \]
因为三角形顶点 \(v\) 是 cube 顶点的线性组合 \(v=(1-t)p_0+tp_1\), 我们认为其梯度也是线性组合 \[ G(v) = (1-t)G(p_0) + tG(p_1). \]
2.1.4 结果与改进
在不同分辨率 \(n\) 下运行的结果 (VCI 的 lab):
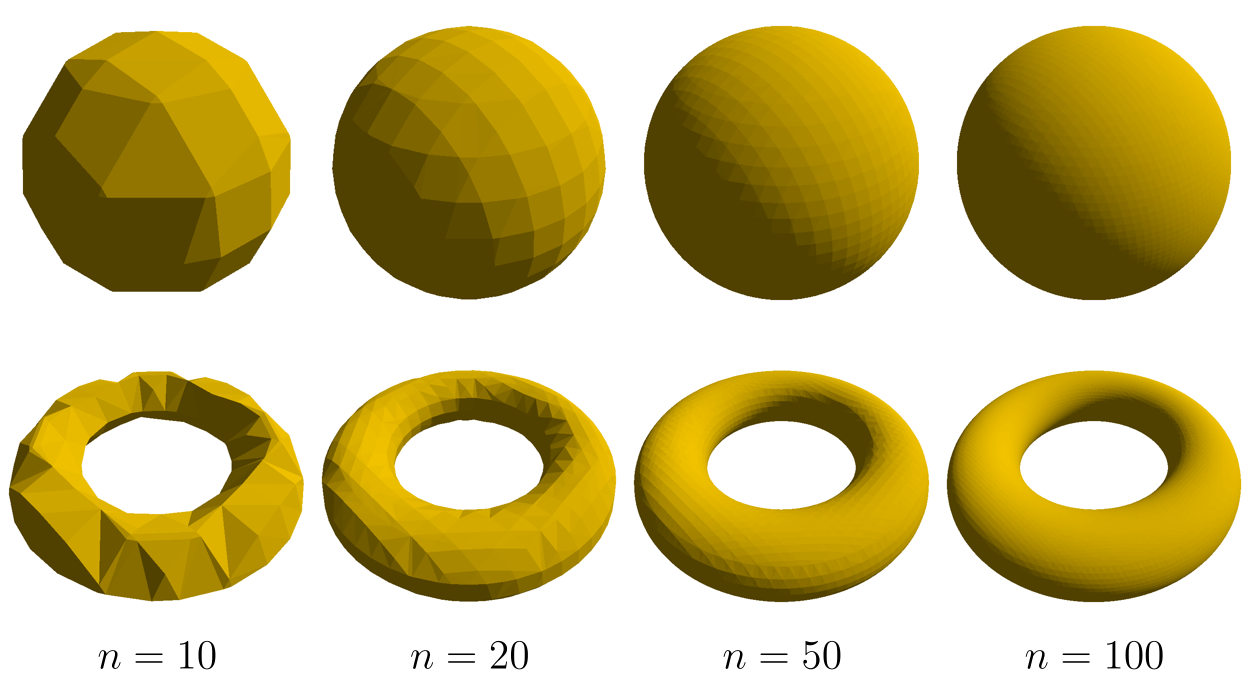
传统的 marching cubes 算法存在一些不足, 比如遍历 \(n^3\) 个立方体的巨大时间开销, 以及对 SDF 的细节还原不足等等. 改进的办法包括利用八叉树等结构实现非均匀采样, 减少空白区域的无效计算; 考虑交点处 SDF 的梯度来提高精度...
2.2 隐式曲面重建
隐式曲面重建将点云转化为 SDF.
2.2.1 SDF 曲面重建
这是一个很直接的算法, 将点云 \(P=\{p_i\}\) 重建成符号距离场 \(F:\R^3\to\R\), 满足 \(F(x)\) 是 \(x\) 到点云的最近的点 \(p_i\) 的带符号距离: \[
F(x) = \lr{x-p_i,n_i},
\] 其中 \(n_i\) 是 \(p_i\) 处的法向量. 如此得到的 \(F\) 的零点集代表了曲面
一个更鲁棒的方法是移动最小二乘法 (MLS, moving least square). 它利用 \(p_i\) 的临近点集, 使用最小二乘法构造局部切平面. 具体来说, 利用八叉树等结构将空间划分为若干部分 \(\{C_j\}\). 在每一部分内, 我们用线性函数 \(f_j(x)=\lr{n,x}+c\) 代表 \(p_i\) 的局部逼近平面, 其参数满足 \[ (n,c) = \argmin_{n,c} \sum_{p_i\in C_j}\bqty{ f_j(p_i)^2 + \lambda \|n-n_{p_i}\|^2 }. \] 误差函数包含两部分, 第一部分 \(f(p_i)^2\) 是平面到点 \(p_i\) 的距离, 第二部分 \(\|n-n_{p_i}\|^2\) 是平面法向量 \(n\) 与 \(p_i\) 处法向量的差距. 用最小二乘法解出 \((n,c)\).
将这些局部的符号距离场 \(f_j(x)\) 加权求和即可得到全局符号距离场: \[ f(x) := \frac{\sum_j\omega_j(x)f_j(x)}{\sum_j \omega_j(x)}, \] 其中权重函数 \(\omega_j\) 在 \(C_j\) 附近为正, 其余地方为零.
2.2.2 Poisson 曲面重建
MLS 法是一个局部的方法. 为了达到更优效果, 可以使用全局的优化方法, 比如 Poisson 曲面重建.
设点云 \(P=\{p_i\}\) 表示了空间区域 \(A\) 的边界曲面 \(\Sigma\) (法向量朝内), 示性函数 \(\chi_A\) 定义为 \[ \chi_A(x) := \Cases{ 1, & x\in A, \\ -1, & x\notin A. } \] 则点云 \(P\) 的法向量场 \(\{n_i\}\) 近似等于 \(\chi_A\) 的梯度场 (\(\chi_A\) 不连续, 但不影响理解). 因此我们的任务就是根据 \(\{n_i\}\) 求出一个连续可微函数 \(\chi:\R^3\to\R\), 使得 \[ E(\chi) = \int \|\nabla\chi(x)-n(x)\|^2 \dd{V} \] 取极小值, 则 \(\chi=0\) 给出了曲面. 由 Euler-Lagrange 方程, \(E(\chi)\) 极小等价于求解 Poisson 方程 \[ \Delta\chi = \operatorname{div}n. \] Poisson 方程的求解需要将空间离散化. 我们构建八叉树 \(O\) 以自适应划分空间, 其每一个叶子节点 \(o\in O\) 都是空间中的立方体, 记其中心为 \(o_c\), 边长为 \(o_w\); 八叉树的根结点包含了区域 \(A\).
在每个节点 \(o\) 上定义基函数: \[ \Align{ B_o:o &\to \R, & B_o(x) := \frac1{o_w^3} B\pqty{\frac{x-o_c}{o_w}}, } \] 其中函数 \(B:\R^3\to\R\) 定义为 \(n\) 次卷积 \(B(x) = (b(x))^{*n}\), \[ b(x) = \Cases{ 1, & \|x\|_{\infty} \leq 1/2, \\ 0, & \textsf{otherwise}. } \] 它们的图像如下:
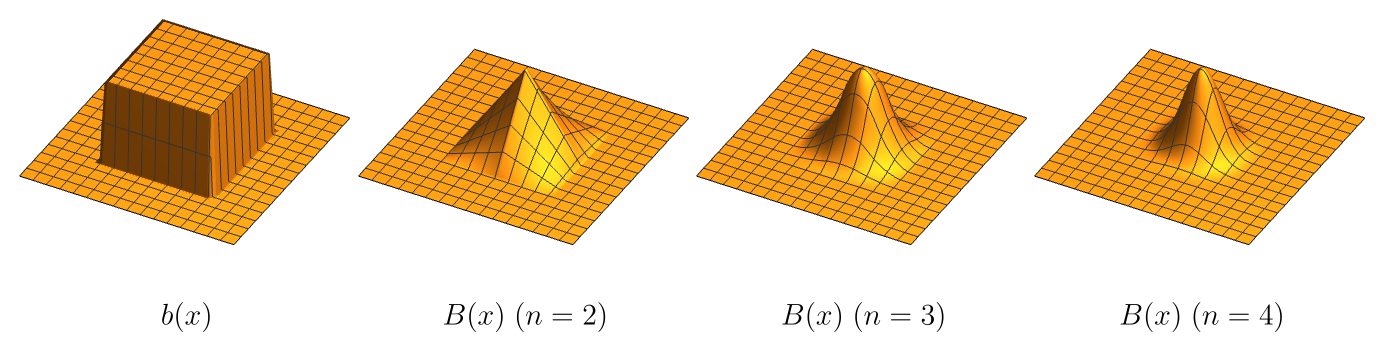
于是能将 \(\chi:\R^3\to\R\) 和 \(n:\R^3\to\R^3\) 表达为基函数的线性组合: \[ \Align{ \chi(x) &\approx \sum_{o\in O}\chi_o B_o(x), \\ n(x) &\approx \sum_{o\in O}n_o B_o(x), \\ } \] 其中 \(\chi_o,n_o\) 是函数在相应叶子结点上的采样值. 于是 Poisson 问题化为 \[ \Align{ \min_{\chi_o} \sum_{o\in O} \lr{\Delta\chi-\operatorname{div}{n},B_o}^2, } \] 解出 \(\chi_o\) 即可.
Poisson 曲面重建是目前应用最广泛的重建算法之一, 其优点是鲁棒性高, 质量好; 缺点是需要法向量, 且无法处理极度稀疏的点云.
2.3 显式曲面重建
显式曲面重建将点云转化为三角形网格.
实际上, 可以先将点云转化为 SDF (如 Poisson 曲面重建), 再用 marching cubes 转化为 mesh. 而本节介绍一些直接将点云转化为 mesh 的方法.
下图展示了使用 Mathematica 中的 ReconstructionMesh
函数进行 mesh 重建的结果. 输入是 bunny 上随机采样的 \(10^4\) 个点, 分别使用 Poisson 曲面重建
(法向量用 MLS 方法计算; 用 marching cubes 提取三角形网格) 和 \(\alpha\)-shape 方法 (采用了不同的 \(\alpha\) 值).

2.3.1 Voronoi 图与 Delaunay 三角剖分
几种显式曲面重建都基于 Voronoi 图与 Delaunay 三角剖分的概念. 它们一般先进行 Delaunay 三角剖分, 然后选取三角剖分的一个子集作为三角形网格.
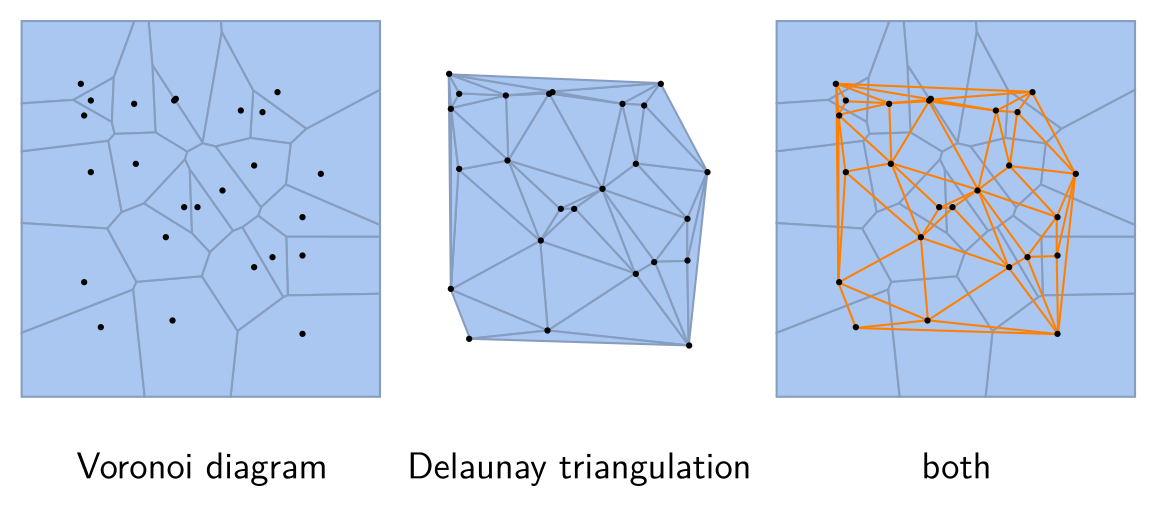
设点云 \(P=\{p_i\}\), 点 \(p_i\) 的 Voronoi 胞腔 (cell) 指的是 \[ V(p_i) := \{x\in\R^3 \mid \|x-p_i\|\leq\|x-p_j\|,\forall j\neq i \}, \] 其中的点到 \(p_i\) 的距离不大于到其他点的距离. Voronoi 区域的边界是一个凸多边形. Voronoi 图 (diagram)指的是所有 \(V(p_i)\) 的并 (上图左), 记作 \(V(P)\).
Delaunay 三角剖分 (triangulation)
- (凸包) \(D(P)\) 的外边界是 \(P\) 的凸包.
- (不可加细) \(D(P)\) 中的三角形的内部不含 \(P\) 中的点.
- (empty circle property) \(D(P)\) 中三角形的外接圆的内部不含 \(P\) 中的点.
- (内角最大) 对于任意 \(P\) 的三角剖分, 它的 "角度向量" 定义为所有内角按照单调递增顺序排列得到的向量. 则在字典序下, \(D(P)\) 的角度向量是所有三角剖分中最大的. 特别地, \(D(P)\) 的最小内角最大.
2.3.2 Alpha shape
Alpha shape 是凸包的推广. 对于 \(\alpha=0\), 定义 \(\alpha\)-闭球为一个点; 对于 \(\alpha=+\infty\), 定义 \(\alpha\)-闭球为闭半空间; 对于 \(0<\alpha<+\infty\), 定义 \(\alpha\)-闭球为半径为 \(\alpha\) 的闭球.
点云 \(P\) 的 \(\alpha\)-shape 是 \(\R^3\) 中的一个以 \(P\) 中某些点为顶点的多面体, 其表面是三角形网格 \({\cal K}\), 满足:
- 对 \(P\) 中任意三个点组成的三角形 \(T\), \(T\subset{\cal K}\) 当且仅当存在 \(\alpha\)-闭球 \(B\) 与 \({\cal K}\) 的交集为 \(T\).
《离散几何处理与应用》中打了一个形象的比方. 点云 \(P\) 的 \(\alpha\)-形可以描述点云的 "形状". 想象 \(\R^3\) 中充满了冰淇淋, \(P\) 中的点是巧克力. 用半径为 \(\alpha\) 的球形勺子尽可能挖去冰淇淋, 而不碰到巧克力. 剩下的部分就是点云的 "形状".
Alpha shape 可能凸, 也可能非凸, 甚至可以不连通. 参数 \(\alpha\) 越小, \(\alpha\)-形越能反映 \(P\) 的细节信息. 然而如果 \(\alpha\) 太小了, 那么 \(\alpha\)-形为空. 当 \(\alpha=+\infty\) 时, \(\alpha\)-形就是 \(P\) 的凸包. 对于合适大小的 \(\alpha\), \(\alpha\)-形的表面可以作为 \(P\) 的三角剖分. 下图展示了从环面 (内外半径分别为 \(1/2,1\)) 上随机采样 \(10^3\) 个点所得的 \(\alpha\)-形.
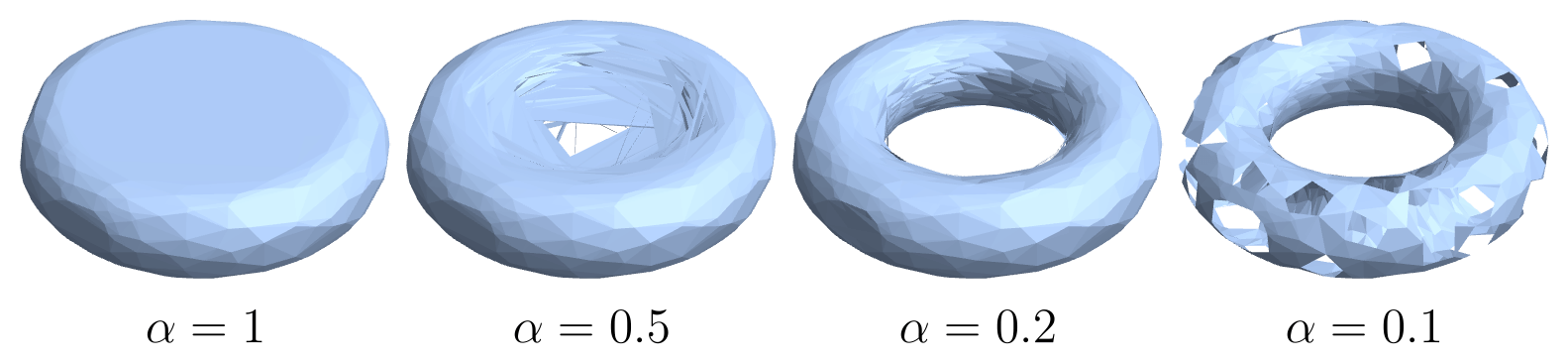
然而构建点云的 \(\alpha\)-形的计算量很大, 而且需要选择合适的 \(\alpha\), 因此它不适合大规模的点云曲面重建.
2.3.3 Power crust
原论文: Nina Amenta, Sunghee Choi, Ravi Krishna Kolluri, The Power Crust.
Power crust 算法能够处理各种输入 (包括空洞、高噪声和尖锐物体), 是当下显式曲面重建的主流算法之一.
3D Vision with Transformers: A Survey - Scientific Figure on ResearchGate. Available from: https://www.researchgate.net/figure/arious-3D-representations-of-the-Stanford-bunny-22-The-projection-based-3D_fig1_362567752 [accessed 25 Feb 2025]↩︎
这实际上要求 mesh 是可定向的 (orientable), 即曲面有正反两个面. 大部分常见曲面 (如平面, 球面, 环面) 都可定向. Möbius 带和 Klein 瓶都只有一个面, 是不可定向的. 可定向等价于曲面拥有连续的单位法向量场.↩︎
这也要求曲面可定向.↩︎
点云 \(P\) 的一个三角剖分指的是以 \(P\) 为顶点集的三角形网格.↩︎