几何重建
要想在计算机中对真实场景进行建模, 最常用的方法是先用 3D 传感器等设备得到点云, 然后把点云转化为表达能力更强 / 更易处理的 3D 表示方法, 比如三角形网格和 SDF. 这两种转换分别称为显示 / 隐式曲面重建, 如下所示. \[ \xymatrix@!{ &&& *[F-,]{\textsf{三角形网格}} \\ *[F-,]{\textsf{实际场景}} \ar[r]^-{\textsf{传感器}}_-{\textsf{点云配准}} & *[F-,]{\textsf{点云}} \ar@/^1.2pc/@<0ex>[rru]^-{\textsf{显式曲面重建}} \ar@/_1.2pc/@<0ex>[rrd]_-{\textsf{隐式曲面重建}} \\ &&& *[F-,]{\textsf{符号距离场}} \ar@<0.0ex>[uu]^{\substack{\textsf{Marching}\\\textsf{cubes}}} } \]
2 隐式曲面重建
隐式曲面重建将点云转化为 SDF.
2.1 SDF 曲面重建
这是一个很直接的算法, 将点云 \(P=\{p_i\}\) 重建成符号距离场 \(F:\R^3\to\R\), 满足 \(F(x)\) 是 \(x\) 到点云的最近的点 \(p_i\) 的带符号距离: \[
F(x) = \lr{x-p_i,n_i},
\] 其中 \(n_i\) 是 \(p_i\) 处的法向量. 如此得到的 \(F\) 的零点集代表了曲面
一个更鲁棒的方法是移动最小二乘法 (MLS, moving least square). 它利用 \(p_i\) 的临近点集, 使用最小二乘法构造局部切平面. 具体来说, 利用八叉树等结构将空间划分为若干部分 \(\{C_j\}\). 在每一部分内, 我们用线性函数 \(f_j(x)=\lr{n,x}+c\) 代表 \(p_i\) 的局部逼近平面, 其参数满足 \[ (n,c) = \argmin_{n,c} \sum_{p_i\in C_j}\bqty{ f_j(p_i)^2 + \lambda \|n-n_{p_i}\|^2 }. \] 误差函数包含两部分, 第一部分 \(f(p_i)^2\) 是平面到点 \(p_i\) 的距离, 第二部分 \(\|n-n_{p_i}\|^2\) 是平面法向量 \(n\) 与 \(p_i\) 处法向量的差距. 用最小二乘法解出 \((n,c)\).
将这些局部的符号距离场 \(f_j(x)\) 加权求和即可得到全局符号距离场: \[ f(x) := \frac{\sum_j\omega_j(x)f_j(x)}{\sum_j \omega_j(x)}, \] 其中权重函数 \(\omega_j\) 在 \(C_j\) 附近为正, 其余地方为零.
2.2 Poisson 曲面重建
MLS 法是一个局部的方法. 为了达到更优效果, 可以使用全局的优化方法, 比如 Poisson 曲面重建.
设点云 \(P=\{p_i\}\) 表示了空间区域 \(A\) 的边界曲面 \(\Sigma\) (法向量朝内), 示性函数 \(\chi_A\) 定义为 \[ \chi_A(x) := \Cases{ 1, & x\in A, \\ -1, & x\notin A. } \] 则点云 \(P\) 的法向量场 \(\{n_i\}\) 近似等于 \(\chi_A\) 的梯度场 (\(\chi_A\) 不连续, 但不影响理解). 因此我们的任务就是根据 \(\{n_i\}\) 求出一个连续可微函数 \(\chi:\R^3\to\R\), 使得 \[ E(\chi) = \int \|\nabla\chi(x)-n(x)\|^2 \dd{V} \] 取极小值, 则 \(\chi=0\) 给出了曲面. 由 Euler-Lagrange 方程, \(E(\chi)\) 极小等价于求解 Poisson 方程 \[ \Delta\chi = \operatorname{div}n. \] Poisson 方程的求解需要将空间离散化. 我们构建八叉树 \(O\) 以自适应划分空间, 其每一个叶子节点 \(o\in O\) 都是空间中的立方体, 记其中心为 \(o_c\), 边长为 \(o_w\); 八叉树的根结点包含了区域 \(A\).
在每个节点 \(o\) 上定义基函数: \[ \Align{ B_o:o &\to \R, & B_o(x) := \frac1{o_w^3} B\pqty{\frac{x-o_c}{o_w}}, } \] 其中函数 \(B:\R^3\to\R\) 定义为 \(n\) 次卷积 \(B(x) = (b(x))^{*n}\), \[ b(x) = \Cases{ 1, & \|x\|_{\infty} \leq 1/2, \\ 0, & \textsf{otherwise}. } \] 它们的图像如下:
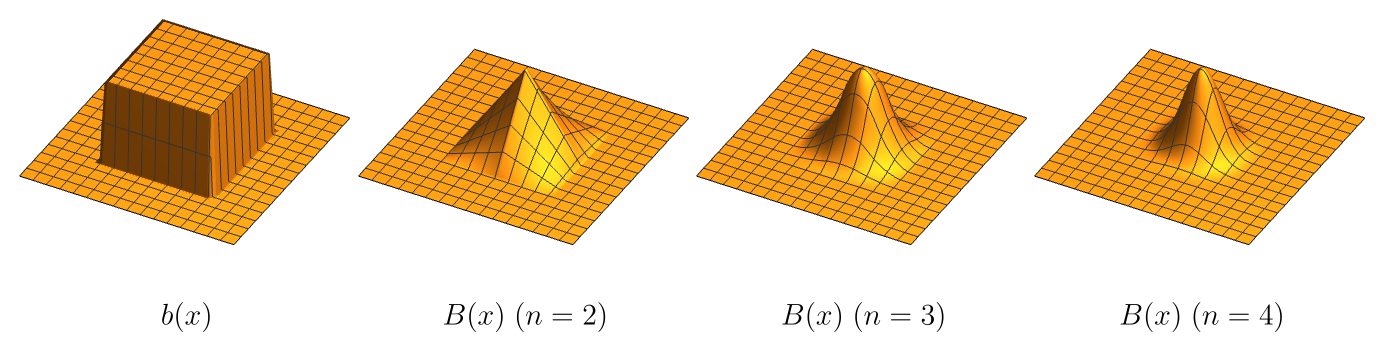
于是能将 \(\chi:\R^3\to\R\) 和 \(n:\R^3\to\R^3\) 表达为基函数的线性组合: \[ \Align{ \chi(x) &\approx \sum_{o\in O}\chi_o B_o(x), \\ n(x) &\approx \sum_{o\in O}n_o B_o(x), \\ } \] 其中 \(\chi_o,n_o\) 是函数在相应叶子结点上的采样值. 于是 Poisson 问题化为 \[ \Align{ \min_{\chi_o} \sum_{o\in O} \lr{\Delta\chi-\operatorname{div}{n},B_o}^2, } \] 解出 \(\chi_o\) 即可.
Poisson 曲面重建是目前应用最广泛的重建算法之一, 其优点是鲁棒性高, 质量好; 缺点是需要法向量, 且无法处理极度稀疏的点云.
3 显式曲面重建
显式曲面重建将点云转化为三角形网格.
实际上, 可以先将点云转化为 SDF (如 Poisson 曲面重建), 再用 marching cubes 转化为 mesh. 除此之外, 本节还会介绍一些直接将点云转化为 mesh 的方法.
下图展示了使用 Mathematica 中的 ReconstructionMesh
函数进行 mesh 重建的结果. 输入是 bunny 上随机采样的 \(10^4\) 个点, 分别使用 Poisson 曲面重建
(法向量用 MLS 方法计算; 用 marching cubes 提取三角形网格) 和 \(\alpha\)-shape 方法 (采用了不同的 \(\alpha\) 值).

3.1 Marching Cubes
Marching cubes 算法将空间中的 SDF 转化为三角形网格.
原论文: Marching cubes: A high resolution 3D surface construction algorithm.
3.1.1 想法
我们首先将空间离散化为 \(n^3\) 个边长为 \(d\) 的正方体 grid (下图左). 如果正方体足够小, 且曲面 \(\Sigma\) 足够光滑, 那么曲面 \(\Sigma\) 与每个正方体的交集应可以用若干三角面片近似 (下图右, 橙色的球面和正方体的交集近似为一个梯形, 可由两个三角形拼成).
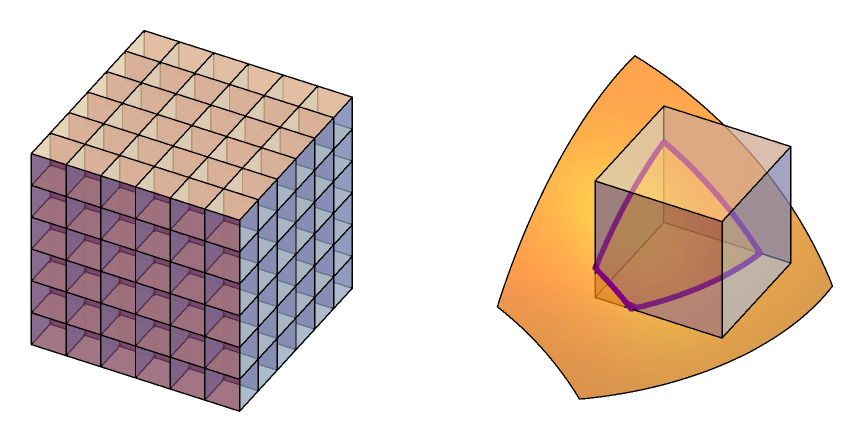
具体来说, 对于一条边 \(e=(p_0,p_1)\), 如果 \({\sf SDF}(p_0)\cdot{\sf SDF}(p_1)\leq0\), 我们就认为曲面 \(\Sigma\) 与边 \(e\) 有一个交点. 由于每个顶点的 SDF 都有两种情况 (正或负), 一个正方体一共有 \(2^8=256\) 种情况; 模去对称性后剩下 \(15\) 种情况: (图源 Wikimedia)

我们不妨假设 SDF 在边 \(e\) 上近似为线性函数, 则交点的坐标为 \[ v = \frac{-F_1}{F_0-F_1} p_0 + \frac{F_0}{F_0-F_1} p_1, \] 其中 \(F_i={\sf SDF}(p_i)\), \(i=0,1\).
该算法逐个遍历每个正方体, 计算完一个后行进到下一个, 故得名 "行进立方体" (marching cubes).
3.1.2 查表
在实现上, 如何快速确定哪些边上有交点/哪些交点属于同一个三角形? 答案是查表.
构造一个 \(8\) 位二进制数 \(\sf vertexState\), 其第 \(i\) 位表示第 \(i\) 顶点的 SDF 是否大于零. 用 \(\sf vertexState\) 作为索引查表, 得到一个 \(12\) 位的二进制数 \(\sf edgeState\), 它的第 \(i\) 位表示第 \(i\) 条边上是否有要生成顶点.
计算出交点坐标后, 再次利用 \(\sf vertexState\) 作为索引, 查另一张表, 得到一个集合 \[ \{(i_1,j_1,k_1),(i_2,j_2,k_2),\dots\}, \] 集合的每一个元素 \((i,j,k)\) 代表一个三角形, \(i,j,k=1,\dots,12\) 分别表示三角形顶点所在的边. 由此便得到了该正方体中的所有三角形面片.
因此, 算法需要两张长度为 \(2^8=256\) 的表, 分别给出 edge state 和 set of triangles.
3.1.3 法向量
最后, 我们还需要计算三角形顶点处的法向量. 因为有 SDF, 我们可以直接利用 SDF 的梯度计算法向量, 而无需在 mesh 上进行插值.
首先计算 cube 顶点 \(p=(i,j,k)\) 处的梯度 \(G(i,j,k)\). 由 central difference 公式, 梯度的三个分量分别为 \[ \Align{ G_x(i,j,k) &= \frac{G(i+1,j,k)-G(i-1,j,k)}{2d}, \\ G_y(i,j,k) &= \frac{G(i,j+1,k)-G(i,j-1,k)}{2d}, \\ G_z(i,j,k) &= \frac{G(i,j,k+1)-G(i,j,k-1)}{2d}. } \]
因为三角形顶点 \(v\) 是 cube 顶点的线性组合 \(v=(1-t)p_0+tp_1\), 我们认为其梯度也是线性组合 \[ G(v) = (1-t)G(p_0) + tG(p_1). \]
3.1.4 结果与改进
在不同分辨率 \(n\) 下运行的结果 (VCI 的 lab):
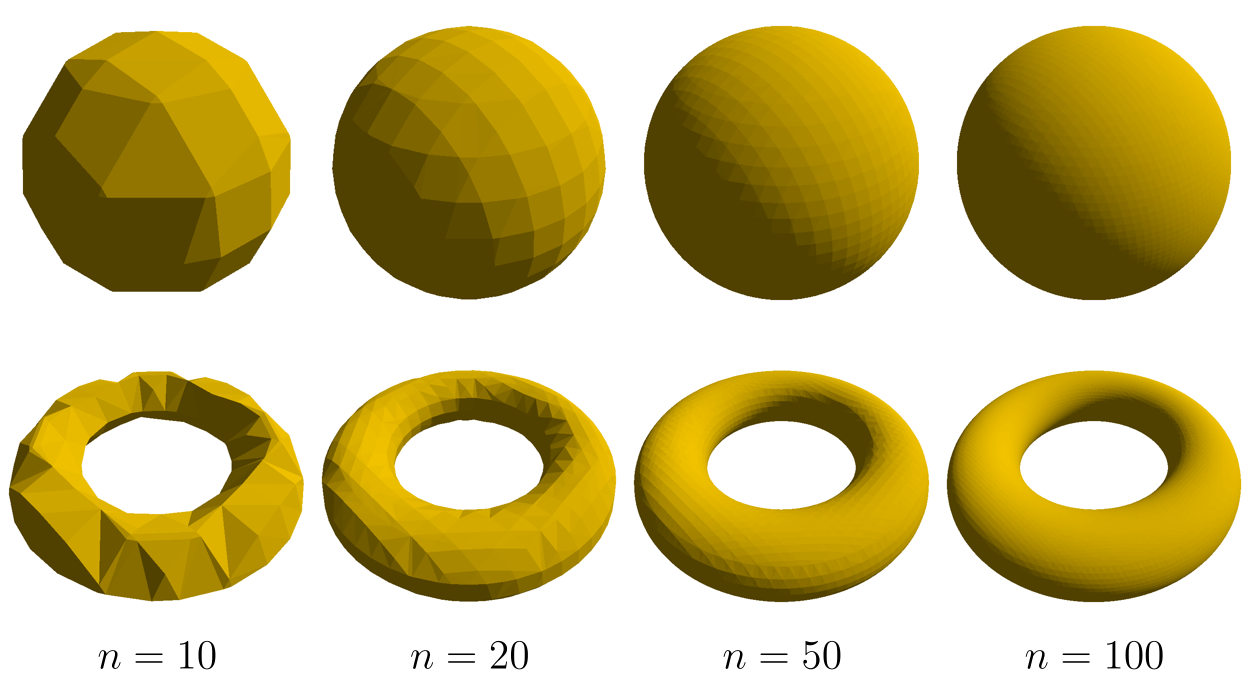
传统的 marching cubes 算法存在一些不足, 比如遍历 \(n^3\) 个立方体的巨大时间开销, 以及对 SDF 的细节还原不足等等. 改进的办法包括利用八叉树等结构实现非均匀采样, 减少空白区域的无效计算; 考虑交点处 SDF 的梯度来提高精度...
3.2 Voronoi 图与 Delaunay 三角剖分
后面的几种显式曲面重建都基于 Voronoi 图与 Delaunay 三角剖分的概念. 它们一般先进行 Delaunay 三角剖分, 然后选取三角剖分的一个子集作为三角形网格.
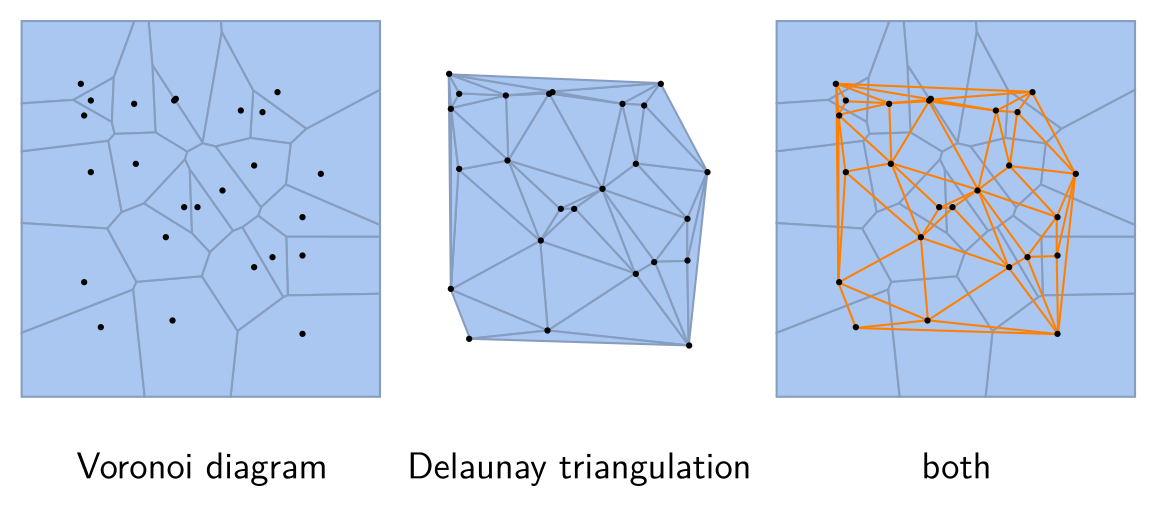
设点云 \(P=\{p_i\}\), 点 \(p_i\) 的 Voronoi 胞腔 (cell) 指的是 \[ V(p_i) := \{x\in\R^3 \mid \|x-p_i\|\leq\|x-p_j\|,\forall j\neq i \}, \] 其中的点到 \(p_i\) 的距离不大于到其他点的距离. Voronoi 区域的边界是一个凸多边形. Voronoi 图 (diagram)指的是所有 \(V(p_i)\) 的并 (上图左), 记作 \(V(P)\).
Delaunay 三角剖分 (triangulation)
- (凸包) \(D(P)\) 的外边界是 \(P\) 的凸包.
- (不可加细) \(D(P)\) 中的三角形的内部不含 \(P\) 中的点.
- (empty circle property) \(D(P)\) 中三角形的外接圆的内部不含 \(P\) 中的点.
- (内角最大) 对于任意 \(P\) 的三角剖分, 它的 "角度向量" 定义为所有内角按照单调递增顺序排列得到的向量. 则在字典序下, \(D(P)\) 的角度向量是所有三角剖分中最大的. 特别地, \(D(P)\) 的最小内角最大.
3.3 Alpha shape
Alpha shape 是凸包的推广. 对于 \(\alpha=0\), 定义 \(\alpha\)-闭球为一个点; 对于 \(\alpha=+\infty\), 定义 \(\alpha\)-闭球为闭半空间; 对于 \(0<\alpha<+\infty\), 定义 \(\alpha\)-闭球为半径为 \(\alpha\) 的闭球.
点云 \(P\) 的 \(\alpha\)-shape 是 \(\R^3\) 中的一个以 \(P\) 中某些点为顶点的多面体, 其表面是三角形网格 \({\cal K}\), 满足:
- 对 \(P\) 中任意三个点组成的三角形 \(T\), \(T\subset{\cal K}\) 当且仅当存在 \(\alpha\)-闭球 \(B\) 与 \({\cal K}\) 的交集为 \(T\).
《离散几何处理与应用》中打了一个形象的比方. 点云 \(P\) 的 \(\alpha\)-形可以描述点云的 "形状". 想象 \(\R^3\) 中充满了冰淇淋, \(P\) 中的点是巧克力. 用半径为 \(\alpha\) 的球形勺子尽可能挖去冰淇淋, 而不碰到巧克力. 剩下的部分就是点云的 "形状".
Alpha shape 可能凸, 也可能非凸, 甚至可以不连通. 参数 \(\alpha\) 越小, \(\alpha\)-形越能反映 \(P\) 的细节信息. 然而如果 \(\alpha\) 太小了, 那么 \(\alpha\)-形为空. 当 \(\alpha=+\infty\) 时, \(\alpha\)-形就是 \(P\) 的凸包. 对于合适大小的 \(\alpha\), \(\alpha\)-形的表面可以作为 \(P\) 的三角剖分. 下图展示了从环面 (内外半径分别为 \(1/2,1\)) 上随机采样 \(10^3\) 个点所得的 \(\alpha\)-形.
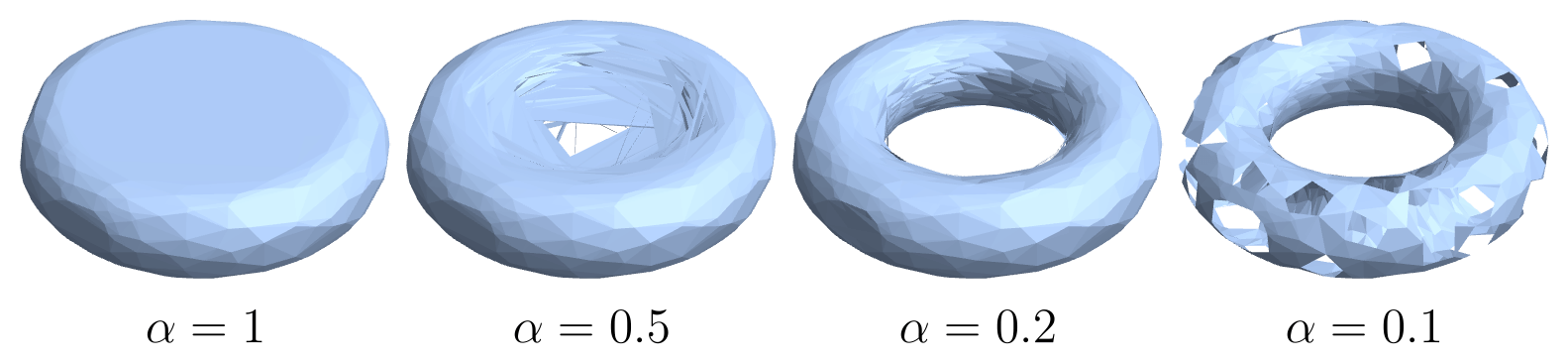
然而构建点云的 \(\alpha\)-形的计算量很大, 而且需要选择合适的 \(\alpha\), 因此它不适合大规模的点云曲面重建.
3.4 Power crust
原论文: Nina Amenta, Sunghee Choi, Ravi Krishna Kolluri, The Power Crust.
Power crust 算法能够处理各种输入 (包括空洞、高噪声和尖锐物体), 是当下显式曲面重建的主流算法之一.